【2023年ノーベル物理学賞】アト秒レーザーで電子の姿を切り取る

ノーベル賞
Point

・アト秒レーザーとは、アト秒という極めて短い時間だけ光るレーザーのこと
・電子はものすごく軽いため超高速で動いている
・アト秒レーザーは、高速に動く電子の一瞬の姿を切り取ることができる 　


２０２３年のノーベル物理学賞がアト秒レーザーに関する内容だったということで、今回は、アト秒レーザーとは何なのか、アト秒レーザーを用いるとどうして電子の動きを観測できるのかについて簡単にまとめる。


アト秒レーザーとは

アト秒レーザーとは、一言で言えば「アト秒という極めて短い時間の間だけ光るレーザー」のことである (図１)。アトという言葉は、ミリやナノなどと同じ接頭語と呼ばれるもので、１０のマイナス１８乗を表す。あえて書き下すと、１アト秒は0.000000000000000001秒であり、０が１８個も並ぶ。１秒間に地球を７周半も回ることができる光であっても、これほど短い時間では、0.3ナノメートルと原子レベルの距離しか進むことができない。アト秒がどれほど短い時間であるかが体感できただろうか。

図１：アト秒レーザー


電子の速さ

次に、アト秒レーザーによる観測の対象となる電子の速さについて見ていく。ここでは、水素原子に注目する。水素原子は、１つの陽子とその周りを公転する１つの電子から成る (図２)。ここで、電子はどれくらいのスピードで公転しているかご存じだろうか。電子の質量は約 9\times10^{-31} kgとものすごく軽いため、そのスピードはとてつもなく速い。具体的には、水素原子の場合、電子のスピードは2000 km/s以上にもなり、約152アト秒で陽子の周りを一周する (末尾の導出を参照)。つまり、電子の運動の時間スケールはアト秒レベルなのである。そしてここに、アト秒レーザーを使う利点がある。

図２：水素原子中の電子が公転するのにかかる時間


電子の一瞬の姿を切り取る

さて、今年のノーベル物理学賞の記事によると、アト秒レーザーは「電子の動きを観測することを可能にした」とある。これを理解するカギとしてストロボ撮影が挙げられる。図３は、飛び跳ねるバスケットボールを４０ミリ秒のストロボライトで撮影した画像である。ストロボ撮影とは、カメラを開けっ放しにした状態で、フラッシュをパッパッと一瞬だけ何度も光らせることによって、素早く運動する物体の姿を可視化する撮影手法である。

図３：バスケットボールのストロボ撮影(Wikipediaの“Bouncing ball”を一部改変)

　なぜこんなことが可能なのかというと、ボールの動きの時間スケールがミリ秒レベルだからである。つまり、ボールは４０ミリ秒の間はほとんど移動しないため、４０ミリ秒の光を当てればその一瞬の姿を切り取ることができるというわけだ。逆に言えば、４０ミリ秒よりもずっと長く光る光を当てると、ボールの動きは平均化されてしまい、一瞬一瞬の姿を切り取ることはできなくなる。


　それでは、これを電子とアト秒レーザーの場合に適用してみよう。前述の水素原子の例では、電子が１周するのにかかる時間が152アト秒であった。つまり、電子は152アト秒よりもずっと短い時間の間はほとんど動かないとみなせる。そのため、アト秒の時間だけ光るレーザーを電子に照射すれば、電子の一瞬の姿を切り取ることができるというわけだ。そして、ストロボ撮影のように、アト秒レーザーを何度も照射すれば、「電子の動きを観測することが可能」なのである。


　ミクロの世界のリアルタイムの動きを知るには、これまでコンピュータのシミュレーションや頭の中の想像に頼るしかなかった。しかし、アト秒などのごく短い時間だけ光るレーザーを発明したことで、科学者たちは実験的にミクロの世界の動画を撮影することができるようになった。今まで見えないものが見えるようになったことは、たしかにノーベル賞を受賞するにふさわしい快挙と思われる。




【付録】電子が陽子の周りを１回転するのにかかる時間の導出

水素原子中の電子が、陽子の周りを１回転するのにかかる時間を古典力学的に導出する方法を示す。といってもそんなに難しくなく、単純に電子が感じるクーロン力と遠心力のつり合いの式を考えればよい。つまり

  \displaystyle\frac{e^2}{4\pi\varepsilon_0 a_0^2}=m_e\frac{v_e^2}{a_0}

と表せる。
ここで、 e : 電荷素量、 \varepsilon_0 : 真空の誘電率、 a_0 : 水素原子の半径、 m_e : 電子の質量、 v_e : 電子の速度とした。少し専門的になってしまうが、水素原子の半径 a_0 はここでは1s軌道に対応する半径、つまりボーア半径とする。
上の式を電子の速度 v_e の式で表すと

  \displaystyle v_e=\frac{e}{\sqrt{4\pi\varepsilon_0 a_0 m_e}}

となる。
この式にそれぞれの定数の値を代入すると電子が回る速度は

  \displaystyle v_e \sim 2187 \ \mathrm{km/s}
と求まる。
電子が陽子の周りを１回転する時間 T は、円周を速度で割れば求まる。
  \begin{split} \displaystyle T=\frac{2\pi a_0}{v_e} \ \sim 152 \end{split} アト秒

円偏光の作り方《１/４波長板 》

光学
Point

・直交する２つの直線偏光の位相を１/４波長ずらすと円偏光になる
・複屈折結晶を用いれば、任意の位相差を与えることができる
・直線偏光を円偏光に変換する光学素子を１/４波長板という 　


円偏光を作る方法をネットで調べてみると、数式や専門用語を使った説明が多く見受けられる。そこで、この記事では、極力イラストを用いてより直観的な説明を試みる。

はじめに、直線偏光が円偏光に変換される際のメカニズムをそれぞれの偏光に注目して解説する。 次に、この変換を実際に行うために必要となる複屈折結晶と呼ばれる光学素子について見ていく。 最後に、円偏光を作るための様々な手法として、トゥルーゼロオーダー波長板、マルチオーダー波長板、ゼロオーダー波長板について解説する。


直線偏光から円偏光へ

円偏光は基本的に、直線偏光に特別な操作を加えることで得ることができる。この節では、直線偏光が円偏光に変換されるときのメカニズムを解説する。
　直線偏光とは、図１のように、電場が直線的に振動しながら伝わっていく光のことをいう。この図では、後の説明のために、電場を45度傾けて描いている。

図１：直線偏光の電場。
緑の直線が光の進行方向、黒の曲線が直線偏光を表す。

ところで、電場とはベクトルであるため分解することが可能である。そこで、図１の電場を大きさが等しい２つの直交する電場に分解してみよう。図２にその結果を示す。

図２：１つの直線偏光を２つの直線偏光に分解した模式図

見た目が複雑になってしまったが、要は

黒色の直線偏光 ＝ 赤色の直線偏光 ＋ 青色の直線偏光

となっているだけである。


進行方向から2次元的に見ると図３のようになっている。こちらの方が、電場を分解していることが分かりやすいかもしれない。ここまでで言いたいこととしては、直線偏光は複数の直線偏光から構成されたものとして捉えることができるということである。

図３：１つの直線偏光を２つの直線偏光に分解した模式図（2次元版）


それでは、ここから直線偏光を円偏光に変換してみる。先に結論から述べると、円偏光への変換は、赤色と青色の直線偏光の位相を、波長の１/４だけズラすことで達成できる。
　詳しく説明するとまず、図２では、赤色と青色の直線偏光は、山と山、谷と谷の位置が一致しており、位相が揃っている。この位相を波長の１/４（ \lambda/4と表す）だけズラすことで、片方の電場の山ともう片方の電場の節もしくは、片方の電場の谷ともう片方の電場の節の位置を揃えるのである。そうすると、赤色と青色の直線偏光を足し合わせた結果は円偏光になる。


　図４に、赤色の直線偏光を青色の直線偏光に対して \lambda/4 だけ遅らせたときの結果を示す。赤と青を足し合わせた黒色の曲線は確かにくるくると回転しており、円偏光となっていることが分かる。なぜこうなるのかというと、赤色と青色の位相がズレたことで、赤が小さくなれば青が大きくなり、逆に、赤が大きくなれば青が小さくなりというように互いを補い合うことで、常に一定の電場強度が回転しながら維持されるからである。

図４：円偏光の電場

　ちなみに、赤色の直線偏光を逆に \lambda/4 だけ進めたときは、円偏光の回転方向は逆回転となる。キラル物質と呼ばれる特別な物質では、円偏光がどっち回りかによって光の吸収にしやすさが異なるという性質がある。これを円二色性といい、回転方向はマニアックな世界では結構重要だったりする。


位相を \frac{\lambda}{4}だけズラすには？

２つに分解した直線偏光の位相を \lambda/4 だけズラせば、円偏光ができることを述べた。それではこの \lambda/4 ズラすという操作を実際に行うにはどうすればよいだろうか。これには、「複屈折結晶」と呼ばれる特別な結晶を用いる。複屈折結晶とはその名の通り複数の屈折率を持つ結晶で、代表的な物としては方解石、水晶、液晶などが挙げられる。

　複屈折結晶の屈折率は、結晶に入射する光の偏光方向によって変わる。具体的には、図５のように、複屈折結晶にはfast軸とslow軸と呼ばれる方向があり、偏光方向がfast軸と平行なときは屈折率が小さい一方、slow軸と平行なときは屈折率は大きくなる。ここで、光の速度は屈折率に反比例するため、fast軸と平行な光は速く進む一方、slow軸と平行な光は遅れることになる。これが、それぞれの軸がfast軸とslow軸と呼ばれる理由である。

図５：複屈折結晶のfast軸とslow軸

　既に気づいたかもしれないが、この方向によって光の速度が違うという性質こそ、位相を \lambda/4 ズラすという操作を行うのに必要なものとなる。なぜなら、この結晶に図２で示したような光を通せば、速度の違いにより、赤色と青色の直線偏光の間に位相差をつけられることになるからである。結晶の厚みを調整すれば、どれだけ位相差がつくかが変わるので、位相差がぴったり \lambda/4 となるような厚みを設計すればよい。このように、２つの直交した直線偏光に特定の位相差を与える光学素子を波長板とよぶ。与える位相差が \lambda/4 な波長板を特に１/４波長板という。読み方は、「しぶんのいちはちょうばん」と言うことが多い気がする。


様々な位相差の与え方

ここまで、ぴったり \lambda/4 の位相差を与える波長板を使うことで、直線偏光を円偏光に変換できるということを解説した。 しかし、 \lambda/4 の位相差を与える方法は他にも複数存在し、それぞれに異なる種類の波長板が対応している。ここでは、トゥルーゼロオーダー波長板、マルチオーダー波長板、ゼロオーダー波長板の３種類を紹介する。


トゥルーゼロオーダー波長板
この波長板は前節で述べた説明と全く同じ原理を用いている。つまり、１枚の複屈折結晶に光を通すことで、fast軸およびslow軸に平行な成分にぴったり \lambda/4 の位相差を与えるというシンプルな方法である（図６）。

図６：トゥルーゼロオーダー波長板による位相変化。赤色と青色の光の波長は同じで、偏光は直交しているとする。

　トゥルーゼロオーダー波長板の特徴として、結晶の厚みが薄いことが挙げられる。例えば、代表的な複屈折結晶である水晶（石英）を材料とした800 nm用の１/４波長板の厚みは22 μmである(末尾の付録を参照)。ここまで薄いと破損しやすくなるため取り扱いが難しいが、その分、波長依存性や温度依存性が低いなど性能は３種類の中で一番良い。


マルチオーダー波長板
円偏光を作るには、直交する２つの直線偏光にぴったり \lambda/4 の位相差を与える必要があるように思われる。しかしよく考えてみると、ぴったり \lambda/4 でなくても、 \lambda/4+m\lambda ( m はゼロ以外の整数)の位相差でも円偏光にできる。なぜなら波長の整数倍だけ位相をずらしても位相関係は何も変わらないからである。このように、 \lambda/4 に加えて波長の整数倍だけ余計に位相を与える波長板をマルチオーダー波長板という（図７）。余計に位相差を与えるということは、トゥルーゼロオーダー波長板よりも厚みを大きくすることができる。このため、取り扱いはしやすくなるが、厚みが増した分、波長依存性や温度依存性は悪くなってしまう。
　ちなみに、マルチオーダーと呼ばれる理由は m\lambda だけ追加で位相を与えるからである。トゥルーゼロオーダー波長板は m=0 なのでゼロオーダーとよばれる。

図７：マルチオーダー波長板による位相変化。mはゼロ以外の整数とする。


ゼロオーダー波長板
上２つの波長板は、波長板の厚み自体がどれだけの位相差を与えるかに関わっていた。一方、ゼロオーダー波長板では、結晶の厚み自体ではなく、厚みの差で \lambda/4 の位相差を与えるという上２つとは異なる方式を採用している。

図８：ゼロオーダー波長板による位相変化

　はじめから解説していくと、まず、図８のように厚みがわずかに異なる２つの複屈折結晶を用意する。そして、１枚目の結晶のslow軸を青色の光の偏光方向と平行に設置することで、青色の光を遅らせる。次に、２枚目の結晶を１枚目とは90度傾けて、slow軸が赤色の光の偏光方向と平行になるように設置することで、今度は赤色の光を遅らせる。このとき、２枚目の結晶の厚みが１枚目の結晶よりもわずかに大きいと(石英, 800 nmの場合は22 μm)、最終的に赤色が \lambda/4 だけ遅れることになる。つまり、それぞれの結晶によって与えられる位相差の大部分が相殺され、厚みの差に相当する位相差だけが最終的に残るのである。この相殺の効果は波長依存性や温度依存性にも良い効果をもたらすため、ゼロオーダー波長板はマルチオーダー波長板よりも高い性能をもつ。ただし、値段はそれに見合ったものとなる。ちなみに図８では、２つの複屈折結晶は距離を離して描いたが、実際はほとんどくっついた状態で一体となって売られている。


以下のソーラボ社では、ここで紹介したマルチオーダー波長板とゼロオーダー波長板が販売されている。実物の写真や、より詳細なスペックが得られるので参考にしてほしい。 www.thorlabs.co.jp



付録：トゥルーゼロオーダー波長板の厚みの導出法
水晶（石英）の800 nmにおける屈折率は、 n_\mathrm{fast}=1.5383 と n_\mathrm{slow}=1.5472 である。ここで、 n_{\mathrm{fast}} と n_{\mathrm{slow}} はそれぞれ偏光方向がfast軸およびslow軸に平行な光の屈折率とする。 屈折率が異なると結晶中での光の速度が変わるため、２つの光が結晶を抜け出るまでの時間に差が生じる。結晶通過後にこれらの光の間で \frac{\lambda}{4}=200\ \mathrm{nm} の位相差をつけるには、この時間差の間に、先に結晶から抜けるfast軸に平行な光が真空中を200 nm先に進んでいればよい。結晶の厚みを d とすると、結晶を抜け出る時間差は

  \displaystyle\frac{d}{\frac{c}{n_\mathrm{slow}}}-\frac{d}{\frac{c}{n_\mathrm{fast}}}

と表せる。この時間の間にfast軸に平行な光が真空中を200 nm進めばいいので

  \displaystyle c\times\left(\frac{d}{\frac{c}{n_\mathrm{slow}}}-\frac{d}{\frac{c}{n_\mathrm{fast}}}\right)=200\ \mathrm{nm}
という式が成り立つ。これを解くと、
  \displaystyle d=\frac{200\ \mathrm{nm}}{n_\mathrm{slow}-n_\mathrm{fast}}

である。ここに、石英の屈折率の値を代入すると結晶の厚みは22 μmと求まる。

Blu-rayがDVDよりも大容量な理由《光の波面》

光学
Point

・波面とは、波の位相が揃った面のこと
・光は波面に対して垂直な方向に進む
・光の波長が短いほど集光点を小さくできる 　


今回は、回折シリーズの３回目として波面と呼ばれるものについて取り上げる。
光には波面という性質があり、この波面の形を調べると、光が次にどのような動きを示すのかを予想することができる。特に、この考え方をレンズに対して適用すれば、波としての光が発散や収束する理由を上手く説明することができる。さらにこの考え方を発展させれば、Blu-rayディスクがCDやDVDよりも大容量である理由についても説明することが可能となる。


光の波面とは

まずは波面とは何かについて見ていく。図１に、横向きに進む光の内部を拡大したイメージ図を示す。光は進行方向とは垂直な方向に幅を持っており、この幅の分だけ、電場（と磁場）が空間的に広がって存在している。ここで、それぞれの電場がもつ位相に注目したとき、位相が同じ点をつなげてできる面のことを「波面」と呼ぶ。

図１：光の波面。山と谷の波面のみ示した。
図１では、点線を用いて山と谷での４つの波面を示した。山や谷は特に重要ではなく、それら以外での位相をつなげた面も波面である。また、図では波面が「線」で表されており、「面」ではないと思われるかもしれないが、立体的に考えれば位相をつなげた点の集まりは「面」となることが分かるだろう。今回の場合だと、波面はちょうど図２のように光の断面に現れる。
図２：立体的な光の波面


波面と光の進行方向

波面の正体が分かったところで、次に波面に関する重要な性質を説明する。その性質とは、光は波面に対して垂直な方向に進みやすいというものである。この理由について説明しよう。といっても、これはすでに以前の回折に関する記事で紹介した光の広がりやすさの説明と全く同じになる。復習としてもう一度見ていこう。


図３に、以前の記事で載せた特定の方向に進む素元波どうしの干渉の様子を示す。光の広がりやすさは素元波どうしの干渉によって理解することができる。つまり、図３で上方向の成分は強め合って残る一方、傾きが大きくなるほど素元波どうしは打ち消し合って消えてしまうため、上方向に光が進みやすいということだった。

図３：特定の方向に進む素元波どうしの干渉

ここで、前の記事では特に言及はしていなかったが、図を見ると、横一列に並んだ素元波の中心における位相が３つとも同じとなっている。つまり、このときの波面は素元波の中心（オレンジ色の点）を結んだ横向きの線となる。波面の方向が横向きで、光の進行しやすい方向が上向きなので、確かに２つの向きが垂直な関係になっていることが分かる。 なぜこのような関係になるのかというと、図３に示したとおり、波面に対して垂直な素元波どうしは位相がズレないため、強め合うことができるからである。


波面を歪めると？

ここまでの話では、平面な形をした波面だけを考えてきた。こうした波面が平面状である波を平面波と呼ぶ。光が平面波の場合、上述のように波面と垂直方向に光はまっすぐ進んでいく。それでは、波面が平面ではなく、歪んだ曲面だとしたら光はどう進むことになるだろうか？


図４に、波面の形状が異なる３つの光とそれぞれの進み方を示した。ここで、光は左から右に流れると仮定する。また、黒の点線は波面を表す。
一番左の絵は、波面が平面上にあるため、平面波である。光の進み方を知るには、波面の各点に、波面に垂直な矢印を描くとよい。平面波の場合は、波面の各点で垂直に進む光がすべて同じ右真横に向いている。つまり平面波は右に直進する。
それでは、中央の絵のように、波面が進行方向に対して逆向きに凹んでいた場合はどうなるだろうか。この場合、波面に垂直な矢印を描くと、それぞれの矢印は光の中心に向くことになる。これらの光がそのまま進むと光はある1点で集まることが分かるだろう。つまり、この場合、光は収束する。
右の絵は、波面が逆に進行方向に出っ張った場合を示す。このときは波面に垂直な矢印は外側を向くため、光は発散する。

図４：波面の形状が異なる光の進行方向。点線は波面を表す。


波面を歪める方法

上述の通り、波面が曲面状に歪むと光は収束したり、発散したりする。それでは、どうすれば波面を上述のように歪めることができるだろうか？収束や発散という言葉でピンと来た人もいるかもしれないが、これには凸レンズもしくは凹レンズを用いればよい。


図５に、平面波が凸レンズおよび凹レンズに通過した後の波面の変化を表す。レンズの材料であるガラスは基本的に空気よりも高い屈折率をもつため、ガラス中での光の速度は空気中での光の速度より遅くなる。凸レンズの場合、中心ほどガラスが分厚く、中心から離れるほど薄くなるため、レンズの中心付近を通る光は遅れる一方、中心から離れた光は先に進むことになる。これにより、レンズを通過前に平面上に揃っていた位相にずれが生じ、図５右上のような波面となる。このときの波面形状では、図４で見た通り光は収束することになる。こうした理由から、凸レンズを通過した光は収束するのである。

図５：凸レンズと凹レンズを通過後の波面
凹レンズの場合は逆で、中心ほどガラスが薄く、中心から離れるほど厚くなるため、図５右下のような波面となる。図４より、このときの波面は発散することになる。以上が、レンズによる波面の変化についての解説である。
　光の収束や発散はレンズだけでなく、凹面鏡や凸面鏡を用いても引き起こせる。この場合も、位相の遅れや進みによる波面の変化を考えれば理解することができる。実際に、絵を描いて確かめてみてほしい。


Blu-rayがCDやDVDよりも大容量な理由

最後に、今回の波面の知識を使って、光が収束する際の波長依存性について述べる。さらにそこから、Blu-rayやDVDなどの光ディスクに情報を読み書きするために使われる光の波長の違いが性能にどう関わっているかについて直観的に説明する。


レンズ等を使うと波面は図４の中央の絵のようになり、光は収束する。ここで、波面の各点からやって来る光はある1点（集光点）で収束するように思える。しかし、それぞれの光はあくまでも波面の垂直方向に進みやすいだけで、ある程度の広がりをもっているため、完全に1点には集まらない。つまり、図６のように集光点には幅がある。

図６：レンズによって集光された光

ここで重要な性質として、集光点の幅は用いる光の波長に依存する。言い換えると、レンズ等を使って光をどれだけ小さく収束できるかは、その光の波長によって変わるのである。具体的には、光の波長が小さいほど、集光点を小さくすることができる。その理由を説明しよう。


ここで、前回の記事（光の回折２：光は波なのになぜまっすぐ進むのか - 直観的に理解する科学）で紹介した、波長が短いほど光は広がりづらいという知識を使おう。つまり、波面の各点から生じる光の広がりが大きい場合と小さい場合で集光点の幅がどう変わるのかを考えてみる。
　図７に、波長が長い場合と短い場合での、波面の各点から生じた光を足し合わせたイメージ図を示す。1本1本の光は、波長が長い場合は末広がりになっている一方、波長が短い場合は広がりが小さくほぼ平行になっている。これらの光が重ね合わさると、波長が短いほど集光点の幅が細くなっていることが分かるだろう。

図７：集光点の幅と波長の関係


　光を使って何かに情報を書き込む際には、光を小さく集光できる方が有利である。なぜなら、集光点が細いほど、同じ面積であっても多くの情報を書き込むことができるからである。喩えるなら、ペン先が細いほど細かい字が書けるため、たくさんの文字を紙に書きこめるのと同じである。ということは、用いる光の波長が短いほど記憶媒体の容量を大きくすることができる。
光を使って情報を記録する記憶媒体である光ディスクの中で有名なものとしては、CD、DVD、Blu-rayが挙げられる。それぞれに使われる光の波長は、CDでは780 nm、DVDでは650 nm、Blu-rayでは405 nmである。確かに製品が高性能になっていくほど、波長が短くなっていることが分かる。ちなみにBlu-rayという名前は青色の光(405 nm)を用いていることにちなんでいる。

光の回折２：光は波なのになぜまっすぐ進むのか

光学
Point

・波は波長が長いほど広がりやすく、波長が短いほど直進しやすい
・光は波長が短いためまっすぐ進む 　


今回は、回折シリーズの2回目として光の直進性について取り上げる。懐中電灯の光や、窓から差し込む太陽光に見られるように、光（可視光）は基本的にまっすぐ進む。一方で、光は電磁波と呼ばれる波である。

波といえば、水面の波や音波に見られるように、まっすぐには進まず、空間全体に広がっていくイメージが強い。つまり、もし図１のように壁の向こう側に音源や光源があるとして、音であれば壁を回り込むことができて耳に入ってくるが、光は壁にさえぎられて見ることはできない。

図１：音と光の広がり方の違い
同じ波であってもこの違いはどこから来るのであろうか。実はこれは音と光の波長の違いに秘密がある。今回の記事では、波の広がりやすさと波長の関係について考察しながら、光が直進する理由を解説する。


光の広がりやすさと波長の関係

前回の記事で、波の広がりやすさは素元波の重ね合わせという考え方を使えば理解できることを学んだ。 casual-science-pedia.hatenablog.com

今回は、この考え方を波長の違いという観点から考えてみよう。ちなみに、波長とは波の山から次の山までの長さを表す。画像検索すればすぐに理解できるだろう。


図１に、波長が長いときと短いときにおける素元波どうしの干渉の様子を示す。素元波の進行方向は右上方向とした。

図１：右上方向に進む素元波の干渉

図から明らかなように、波長が長いときは素元波どうしの位相がそれほどずれないため、重なり合っても光はある程度生き残る。一方、波長が短いときは位相のずれが大きく、重なり合うと打ち消し合って光が消えてしまう。つまり、同じ進行方向であっても波長が短いほど、素元波は打ち消し合いやすくなる。
ななめ方向の光が残るということは、広がりやすいということを表す一方、ななめ方向の光が消えてしまうということは、直進しやすいということを表す。つまりまとめると、波長が長いほど光は広がりやすく、逆に波長が短いほど光は直進しやすいことになる。敢えて図にするなら、図２のようになる。

図２：波の広がりやすさと波長の関係


光がまっすぐ進む理由と音波が広がる理由

人間の目に見える光は可視光と呼ばれ、数百ナノメートルというとても小さい波長をもつ。これほどの波長となると、素元波は少し傾いただけで打ち消し合ってしまい、ほとんど直進成分しか残らない。これが、光（可視光）が波であるにもかかわらずまっすぐ進む理由となる。理由を聞いてしまえば、なぁんだという感じだ。

逆に、人の声の波長はだいたい1メートルくらいであり、可視光の波長の100万倍以上にもなる。だから、音波は直進性が低く広がりやすいのである。 光と音波の広がりやすさの理由をなんとなくイメージできただろうか。


電磁波の波長

最後に、可視光以外の波長領域についても述べておこう。可視光は電磁波の中で波長が数百ナノメートル程度の領域を指すが、それ以外の波長にも名称がつけられている。代表的な名称を波長が長い順に列挙すると
・電波
・マイクロ波
・赤外線
・可視光線
・紫外線
・X線
・ガンマ線
が有名だろう。ここで、一番最後の漢字を見るとあることに気づく。電波とマイクロ波は語尾が波 (wave) であるのに対し、赤外線～ガンマ線は語尾が線 (ray)になっているのだ。ただ、この理由は上述の説明を聞けば理解できるだろう。光は波長が長いほど広がりやすく、逆に波長が短いほど直進しやすいのだった。そのため、波長が長い電波やマイクロ波は波のように広がりやすいし、波長が短い赤外線～ガンマ線はまさに線のようにまっすぐ進みやすいのだ。

実際、電波が情報を送る手段として利用されているのは、その広がりやすい性質により遠くまで届きやすいからというのが理由の1つになっている。このように、同じ光であっても波長によって性質が大きく異なるということを知っておくとよいだろう。

光の回折１：スリット幅と光の広がりやすさ《素元波》

光学
Point

・光がスリットを通過したとき、スリットの幅が小さいほど光は広がりやすい
・光の広がりやすさは素元波の干渉で説明できる 　


今回の記事では、光が障害物の裏側に回り込む現象である「回折」について紹介していく。光の回折を説明するための分かりやすい題材として、スリットを使った実験が挙げられる。この記事では、光がスリットを通過すると何が起こるのかをテーマにして、回折現象の直観的なイメージを与えていく。


スリットを通過した光

まずは、図を使ってスリット通過後の光の動きを見ていこう。図１のように、光がスリットを通過すると、光はスリットの幅以上に広がって伝わっていく。これが「回折」である。

図１：幅の異なるスリットを通過した後の光
そして、スリットの幅によって光の広がりやすさは変わる。通過するスリットの幅が大きいほど、光の広がり方は小さくなり、逆に、通過するスリットの幅が小さいほど、光の広がり方は大きくなる。



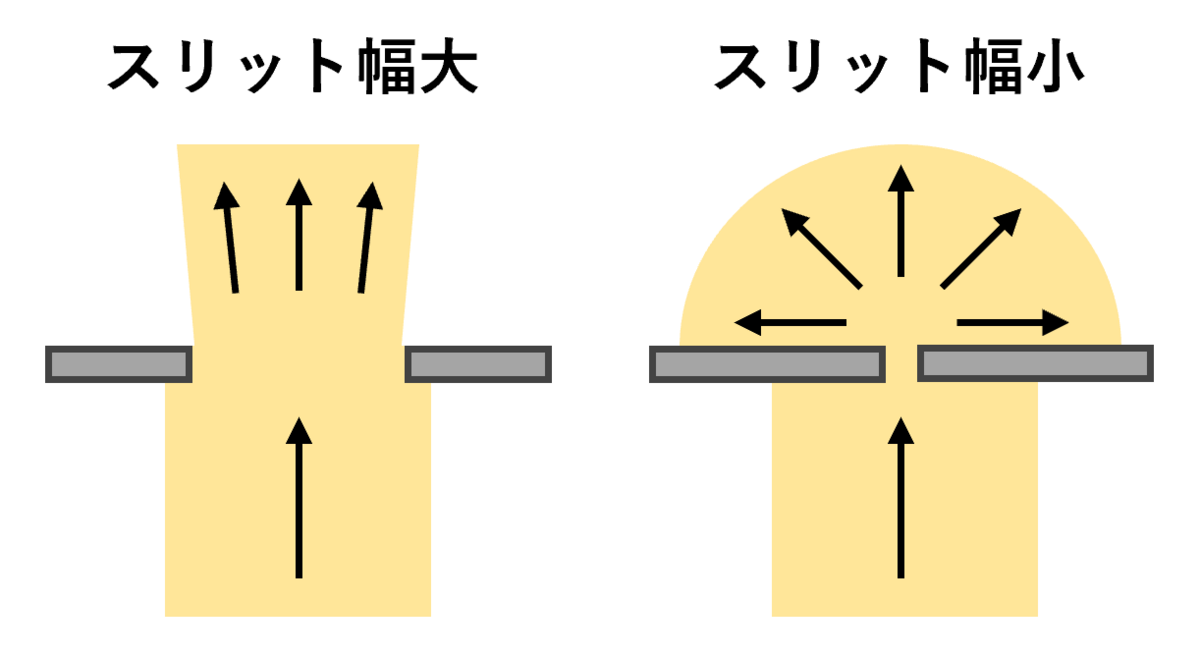
光の広がりやすさをどうやって説明するか

上述のように、スリット幅が大きいときは光は広がりにくく、逆にスリット幅が小さいときは光は広がりやすい。光学では、これらの回折現象を統一的に説明するための方法として「素元波(そげんは)」という考え方が使われる。素元波とはその名が示す通り、波の元となるものであり、物質で言うところの原子みたいなものである。原子が集まって物質ができるように、素元波も複数集まることで1つの合成された波を形成する。この合成波が実際に物理現象として現れてくると考えるのである。ちなみに素元波の形は、発生源を中心に波紋のように同心円状に広がる波をイメージしてもらえばよい。


文字だけでは分かりにくいと思うので、図を使って説明してみる。図３に、スリットを通過後に発生した複数の素元波を示す。

図３：スリットを通過後に発生する素元波
この図では、３つの異なる地点から発生した素元波が同心円状に広がる様子を描いた。これらが合成された結果を調べれば、スリット通過後の光の挙動を理解することができる。(※実際は素元波の個数といった考え方はせず、スリット上での積分を考えるが、今回は分かりやすさを優先する。)


図３では、半円状のあらゆる方向に進む波が一度に描かれているため、合成したらどうなるかパッと見でわかりづらい。そこで図４に、角度の違いによって３つの素元波がどのように干渉するかを表すアニメーションを示した。

図４：角度を変えていったときの素元波の干渉
わかりやすさのため、３つの素元波は異なる色で描き、振動方向は画面と平行な方向に表した。見ての通り、上方向に進む成分は波の位相が揃っているが、角度がななめになるにつれて位相がズレていくのがわかる。つまり、光が進む方向によって素元波の干渉の仕方が異なるのである。


特定の方向に進む波を取り出してみよう。 図５に、上方向に進む成分、ななめ方向に進む成分、さらにななめ方向に進む成分の静止画を示す。

図５：特定の方向に進む素元波どうしの干渉
前述のように上方向に進む成分では、３つの素元波の位相が揃っているため、強め合う干渉が起こる。この強め合いは上方向に進む光が生き残りやすいことを表す。

次に、ななめ方向に進む成分を見ると、３つの素元波がななめになったことで、位相が少しだけズレていることがわかる。このため、これらを合成しても、上方向成分の場合のような完全な強め合いは起こらない。結果として、ななめ方向に進む光は上方向に進む光よりも生き残りづらくなる。

さらにななめ方向となると、位相のズレがかなり大きくなる。この状態で合成しても、ランダムな干渉となるため、光は打ち消しあって消えてしまう。


以上から、光の進行方向が上方向のときに光は一番強くなり、上方向から傾くほど、素元波どうしの打ち消し合いによって光が弱くなるという結論が得られた。



スリット幅と光の広がりやすさ

それでは、この考え方をスリット幅と光の広がりやすさの関係に適用する。ここで、スリット幅は素元波の個数と関係していると考えてみよう。つまり、スリット幅が広いほど発生する素元波の数が多く、逆にスリット幅が狭いほど素元波の数が少ないといった風にイメージするのである。
　素元波の数が多いほど、より多くの位相のズレた波を合成することになるため、少し角度が傾いただけで打ち消し合いが起こりやすくなるのが想像できるだろう。そのため、まっすぐ進む成分がより残りやすく、ななめの成分はより生き残りづらくなる。こういった理由で、スリットの幅が広いほど光が広がりづらくなるのである。
　素元波の数が少ないほど、合成する波の位相のずれは小さくて済むので、ななめの成分は生き残りやすい。スリット幅の小さい極限では、図６のように、発生する素元波の数が１個だけといったイメージを持ってもよい。素元波とは同心円状に広がる波であるため、図６のように素元波が１つだけのような場合、どの方向にも同じ強さの光が伝わる。そのため、スリットが狭いときは、通過した光は大きく広がるのである。

図６：幅の狭いスリットを通過後に発生する１つの素元波


ここまで、素元波が１つや３つなど個数を具体的に与えて回折現象を考えてきた。しかし、厳密な計算をする際には、素元波が連続的に存在すると考え、素元波の個数などというものは本来考えない。しかし、スリットの幅が広いほど素元波の数が多いという考え方はイメージがつきやすいため、今回は直観的な分かりやすさを優先した。素元波同士の干渉を用いた考え方は、その他の回折現象を理解する際にも役立つため、今後の記事でも多用していく。

光が屈折する理由を車を使って説明する《光の屈折》

光学
Point

・光の屈折は車の喩えを使って直観的に説明できる
・光が屈折する理由は物質によって光の速度が異なるため 　


空気から水に向かって光が侵入すると、光が屈折するのは日常目にする光景である。しかし、その理由を説明しようと思うとするとなかなか難しい。そこで、この記事では、光を車に見たてて直観的な説明を試みる。


光の屈折の事前知識

本題に入る前に、光の屈折の特徴について見ていく。図１のように、屈折率が異なる物質の境界に光が到達すると、光は進行方向を変える。この現象を屈折とよぶ。屈折率の関係が n_1 < n_2 の場合は、光は図１のように進行方向が下へ向くように折れ曲がる。

図１：光の屈折 ( n_1 < n_2の場合)

光がなぜ物質の境界で屈折するのかを理解するには、光の速度が屈折率によって変化することを知っておく必要がある。実際、物質中での光の速度を c'とすると、

  \displaystyle c'=\frac{c}{n}

と表される。ここで、 cは真空中での光速、 nは屈折率である。つまり、屈折率 n が大きいほど、光は遅くなる。


図１のように屈折率の関係が n_1 < n_2 の場合は、光が速い領域から遅い領域へ侵入するという状況になる。そこで、以下では、同様の状況を車を使って再現することで屈折という現象を直観的に理解してみよう。


光の屈折を車で説明する

それでは、ここからは光を車に見たてて話しを進めていく。図２に、走っている車を上から見た様子を示す。上側の黒い領域は舗装された道路を表し、下側のまだら模様は舗装されていないダートを表す。車は道路からダートに向かってななめに侵入するとする。ここで、上記の光の状況と同じにするため、車のタイヤが道路からダートに移った瞬間にダート上のタイヤの速度が落ちるとする(実際にそうなるのかは分からないが...)。

図２：道路からダートに向かって走る車


この車がダートに侵入した後の動きを図３に示す。図のようにななめに車が侵入するとまず、片方のタイヤがダート上に移ることになる(図では右輪)。すると、ダート上にある右輪は速度が遅くなる一方で、まだ道路上にある左輪は速度が速いままとなる。この速度差によって車はもともとの進行方向に対して自然と右向きに曲がる。

図３：道路からダートに侵入した車が曲がる様子

つまり、速度の異なる地面にななめから侵入すると車の進行方向が変わるのである。この車の動きは図１の光の屈折とよく似ているのがわかるだろう。これが、車の喩えを使った屈折の説明である。このように、ある現象をまったく別の事柄を使って理解しようとする方法をアナロジーという。


ここまでは、 n_1 < n_2 の場合、つまり速度が速い領域から遅い領域に移る場合について説明してきた。それでは、逆に屈折率が n_1 > n_2 の場合、つまり速度が遅い領域から速い領域に移る場合はどうなるだろうか。 このとき、光は先ほどとは逆に物質の境界に近づくようにに屈折する。実は、このときも車の喩えを使って説明することができるので確かめてみてほしい。(ダートから道路への侵入を考えればよい)

ブリュースター角で光の反射を消す

光学
Point

・ブリュースター角とは、p偏光の反射率がゼロになる入射角
・反射光と透過光のなす角が90度となる
・双極子の振動方向に光が発生しないことから説明できる 　


ブリュースター角とは

以下に示した図は、以前の記事で紹介した入射角に対するp偏光とs偏光の反射率である。

図１：入射角に対するp偏光とs偏光の反射率 ( n_1=1, n_2=2)

赤色のp偏光に注目すると、60°付近に反射率がゼロになる入射角が存在している。このときの入射角をブリュースター角とよぶ。反射率がゼロになるということは、ブリュースター角ではp偏光は100%透過することになる。


ブリュースター角の数式

次に、ブリュースター角の求め方や条件などを定量的に探っていく。p偏光の反射率がゼロになるということは、p偏光のフレネル係数 \rhoをゼロとすればよいだろう。 準備のため、まずはフレネル係数の式変形を行っていく。

  \displaystyle\rho=\frac{n_1\cos\theta_2-n_2\cos\theta_1}{n_1\cos\theta_2+n_2\cos\theta_1}


スネルの公式 ( n_1\sin{\theta_1}=n_2\sin{\theta_2}) を使って屈折率を消去すると

  \displaystyle\rho=\frac{\sin\theta_2\cos\theta_2-\sin\theta_1\cos\theta_1}{\sin\theta_2\cos\theta_2+\sin\theta_1\cos\theta_1}


2倍角の公式 ( \sin2\theta=\sin\theta\cos\theta ) を使うと

  \displaystyle\rho=\frac{\sin2\theta_2-\sin2\theta_1}{\sin2\theta_2+\sin2\theta_1}


和積の公式 ( \sin\alpha\pm\sin\beta=2\sin\frac{\alpha\pm\beta}{2}\cos\frac{\alpha\mp\beta}{2}) を使うと

  \displaystyle\rho=\frac{\sin(\theta_1-\theta_2)\cos(\theta_1+\theta_2)}{\sin(\theta_1+\theta_2)\cos(\theta_1-\theta_2)}


最終的に、以下のように単純な式に変形できる。

  \displaystyle\rho=\frac{\tan(\theta_1-\theta_2)}{\tan(\theta_1+\theta_2)}


この式がゼロとなるには、分子がゼロになるか、または分母が無限大になればよい。分子がゼロとなる場合は、 \theta_1=\theta_2となるが、これは屈折をしていないことになってしまうので不適である。一方、分母が無限大となる場合は、

  \displaystyle\theta_1+\theta_2=\frac{\pi}{2}


が得られる。この式は、反射光(実際には存在しないが)と透過光のなす角が90°であることを表している。図２はこれを模式的に表したものである。

図２：ブリュースター角での反射光と透過光の関係。

続いて、ブリュースター角を求める式を導出する。 \theta_1+\theta_2=\frac{\pi}{2} とスネルの公式 ( n_1\sin{\theta_1}=n_2\sin{\theta_2}) を用いて \theta_2を消去すると

  \begin{aligned} n_1\sin{\theta_1} &= n_2\sin({\frac{\pi}{2}-\theta_1})\\ &=n_2\cos\theta_1 \end{aligned}


\sin \theta_1と \cos \theta_1を \tan \theta_1にまとめて、 \theta_1の式で表すと

  \displaystyle \theta_1=\tan^{-1}\left(\frac{n_2}{n_1}\right)


となる。これがブリュースター角を求める式である。実際に、図1の条件である ( n_1=1, n_2=2) を代入すると、 \theta_1=63^{\circ} が得られ、図１の反射率ゼロでの角度と一致する。


なぜ反射率がゼロになるのか

ここまで、ブリュースター角の性質を説明してきたが、そもそもなぜ特定の入射角でp偏光の反射率がゼロになるのだろうか。実はこれは、さきほど言及した「反射光と透過光のなす角が90°である」ことが効いている。

本題に入る前に、先に反射光の正体について考えてみる。直感的には反射光とは、入射光がそのまま向きを変えて反射した光というイメージが自然だと思われるかもしれない。しかし、ここでは少し見方を変えて、反射光とは入射光によって振動させられた双極子から発生した光としてとらえてみよう。

電磁気学において、振動する双極子からは光が放出されることが知られている。このとき、双極子の振動に対して垂直方向に最も光が発生しやすい一方、振動に平行な方向には光は放出されない。これを図で表すと以下のようになる。

図３：振動する双極子から放出される光の方向分布

これを踏まえて、ブリュースター角ではp偏光の反射率がゼロになるという話に戻ろう。先ほど述べたようにブリュースター角では「反射光と透過光のなす角が90°」になるのであった。p偏光ではこのとき、透過光の偏光方向と反射光の進行方向が平行になる（図２参照）ことが分かるだろう。透過光にさらされた双極子はその偏光方向に振動するため、それに平行な方向に光は発生しない。だから、反射光はゼロになるのである。

まとめると、
　「ブリュースター角において反射光と透過光のなす角は90°となる」
→「このときp偏光では、透過光にさらされた双極子の振動方向が反射光の進行方向と平行になる」
→「双極子振動に平行な方向には光は発生しない」
→「p偏光の反射率はゼロになる」
ということだ。


こう考えると、なぜs偏光では反射率がゼロになる入射角がないかわかるだろう。s偏光では、透過光の偏光方向が反射光の進行方向と平行になることは絶対にないからである。