フレネル係数で遊ぶ１：垂直入射を中心に

Point

　入射光の電場にフレネル係数を掛けると、
　反射光の電場および透過光の電場に変換できる。　

今回はいよいよ光学の分野で最も重要な式の１つであるフレネル係数について見ていく。フレネル係数の応用範囲はかなり広いため、これを理解するだけで光への理解が驚くほど深まるだろう。

フレネル係数とは

図１のように、入射光電場 $E_i$ が物質の境界で反射および屈折し、電場がそれぞれ $E_r$ および $E_t$ に変化したとする。このとき、入射光の電場 $E_i$ を反射光の電場 $E_r$ もしくは透過光の電場 $E_t$ に変換する係数をフレネル係数とよぶ。つまり、反射のフレネル係数を $\rho$ 、透過のフレネル係数を $\tau$ とすると、

$\displaystyle E_r=\rho \cdot E_i \\ E_t=\tau \cdot E_i$

と書ける。
フレネル係数を掛けるだけで変換できるので、とても単純である。

フレネル係数の式

次に、具体的なフレネル係数の式を見ていく。実はフレネル係数は、入射光がp偏光かs偏光かどうかで若干異なってくる。
s偏光の場合、

$\displaystyle\rho=\frac{n_1\cos\theta_1-n_2\cos\theta_2}{n_1\cos\theta_1+n_2\cos\theta_2}, \quad \tau=\frac{2n_1\cos\theta_1}{n_1\cos\theta_1+n_2\cos\theta_2}$

p偏光の場合、

$\displaystyle\rho=\frac{n_1\cos\theta_2-n_2\cos\theta_1}{n_1\cos\theta_2+n_2\cos\theta_1}, \quad \tau=\frac{2n_1\cos\theta_1}{n_1\cos\theta_2+n_2\cos\theta_1}$

と表される。ここで、それぞれの記号は上の図で示したように、 $\theta_1$ : 入射角、 $\theta_2$ : 屈折角、 $n_1$ : 入射側の物質の屈折率、 $n_2$ : 屈折側の物質の屈折率とする。フレネル係数の導出法については、ネット上に分かりやすい解説がたくさん出ているのでここでは割愛する。

フレネル係数を初めて学ぶ人は、式が複雑で難しく思えるかもしれない。なので話を単純化するため、 $\theta_1=\theta_2=0$ 、つまり光が垂直に入射する場合を考える。その場合、p偏光とs偏光の区別がなくなり、

$\displaystyle\rho=\frac{n_1-n_2}{n_1+n_2}, \quad \tau=\frac{2n_1}{n_1+n_2}$

と式がかなり単純になる。
この式に例えば、空気の屈折率 ( $n_1=1.0$ ) と、可視光領域の水の屈折率 ( $n_2=1.3$ ) を代入してみると、 $\rho=-0.13, \quad\tau=0.87$ といった値が得られる。これらの値を入射光の電場に掛ければ、空気から水に垂直に入射した場合の反射光と透過光の電場が得られるというわけだ。

反射後の位相のずれ

上の計算からわかるように、フレネル係数は正負どちらの値も取りうる。もう少し正確に言うと、 $\tau$ は必ず正の値となるが、 $\rho$ は $n_1> n_2$ では正の値、 $n_1$ < $n_2$ では負の値となる。これは何を意味しているのだろうか？

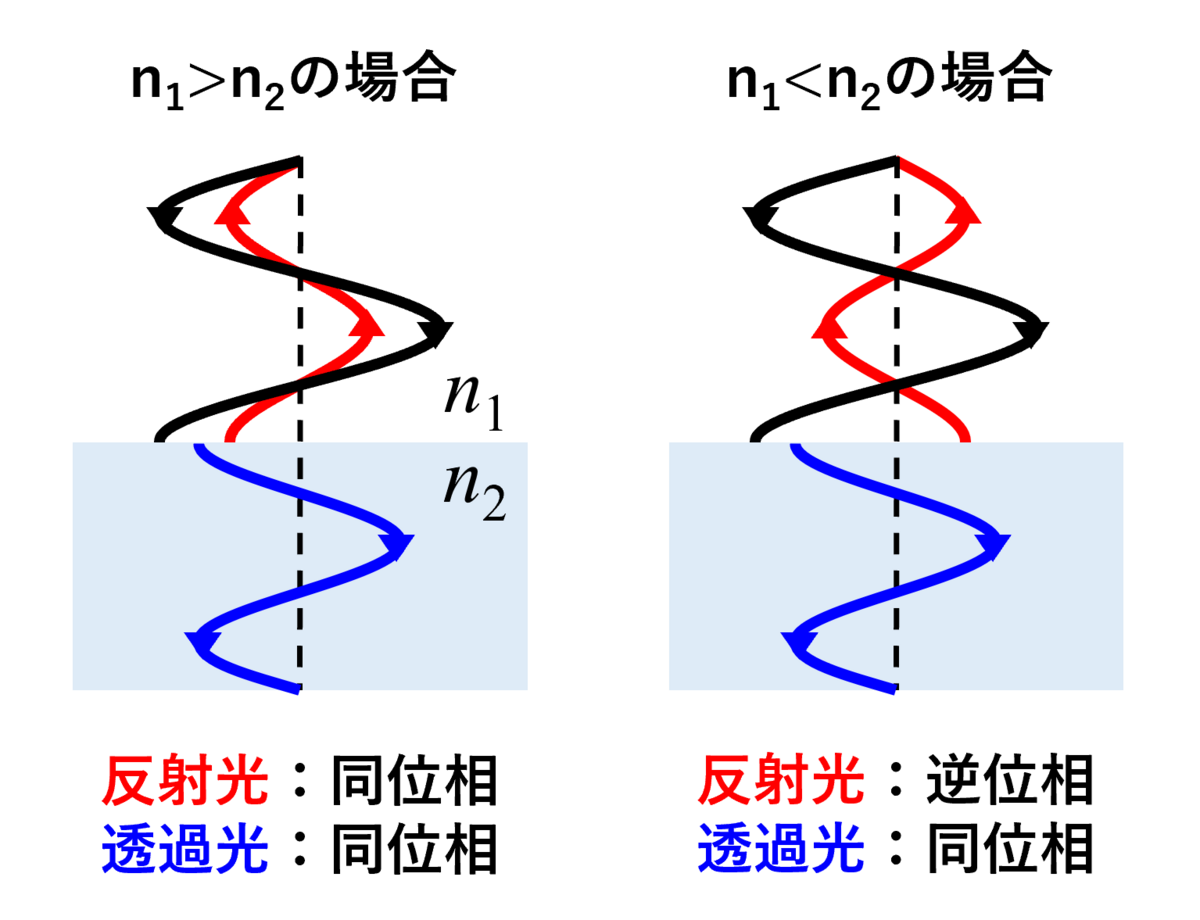
フレネル係数が正または負であるということは、反射光や透過光の位相が入射光と同じかまたは反転するということである。つまり、 $\tau$ は必ず正なので、透過光は必ず入射光と同位相になる。一方で、反射光は $n_1> n_2$ では同位相となり、 $n_1$ < $n_2$ では逆位相となる。実はこの反射光の位相変化は、高校物理で習った自由端反射と固定端反射に対応している。これらをまとめたものを図２に示す。

垂直入射における反射率と透過率

ここまでは「電場」の変化に注目してきた。しかし、われわれが直接観測できるのは電場ではなく、光の明るさやエネルギーに相当する「光強度」である。そのため、フレネル係数を光強度の変化、つまり反射率と透過率に変換できると都合がよい。ここでは、その方法を説明する。

光強度 $I$ は $I=n \varepsilon_0 c E^{2}$ で計算できる。ここで、 $\varepsilon_0$ は真空の誘電率、 $c$ は光速である。入射光、反射光、透過光の強度をそれぞれ $I_0, I_r, I_t$ とおくと、反射率 $R$ と透過率 $T$ は

$\displaystyle R=\frac{I_r}{I_0}=\frac{n_{1} \varepsilon_0 c E_{r} ^{2}}{n_{1} \varepsilon_0 c E_{i} ^{2}}=\frac{E_{r} ^{2}}{E_{i} ^{2}}=\frac{\rho^2 E_{i} ^{2}}{E_{i} ^{2}}=\rho^2=\left(\frac{n_1-n_2}{n_1+n_2}\right)^2$

$\displaystyle T=\frac{I_t}{I_0}=\frac{n_{2} \varepsilon_0 c E_{t} ^{2}}{n_{1} \varepsilon_0 c E_{i} ^{2}}=\frac{n_2}{n_1}\frac{E_{t} ^{2}}{E_{i} ^{2}}=\frac{n_2}{n_1}\frac{\tau^2 E_{i} ^{2}}{E_{i} ^{2}}=\frac{n_2}{n_1}\tau^2=\frac{n_2}{n_1}\left(\frac{2n_1}{n_1+n_2}\right)^2$

となる。
ポイントとしては、反射率は $\rho$ を2乗するだけでよいが、透過率は $\tau$ の2乗に屈折率の比を掛ける必要があるところ。反射率と透過率でなぜこのような違いが出てくるかというと、反射が屈折率 $n_1$ の物質中で完結する現象であるのに対し、透過は屈折率が $n_1$ から $n_2$ への変化を伴う現象だからである。
この式から分かることとして、反射率 $R$ は屈折率の差 $(n_1-n_2)$ が大きいほど上がるということを覚えておこう。普通のガラスの屈折率は1.5くらいで水の屈折率1.3よりも大きいので、空気からガラスへ入射したときの方が、空気から水への入射よりも反射率が大きいといったことが瞬時にわかる。

ちなみに、入射光はすべて反射光と透過光に分かれるため、反射率と透過率を足すと1になるはずである。実際に確かめてみると、

$\begin{aligned} \displaystyle R+T&=\left(\frac{n_1-n_2}{n_1+n_2}\right)^2+\frac{n_2}{n_1}\left(\frac{2n_1}{n_1+n_2}\right)^2 \\ &=\frac{n_1^2-2n_1n_2+n_2^2}{n_1^2+2n_1n_2+n_2^2}+\frac{4n_1n_2}{n_1^2+2n_1n_2+n_2^2} \\ &=\frac{n_1^2+2n_1n_2+n_2^2}{n_1^2+2n_1n_2+n_2^2} \\ &=1 \end{aligned}$

となり、確かに足し合わせると1になる。

ガラス板の透過率

最後に、フレネル係数にちなんだより実践的な話をしておこう。ここでは、光がガラス板を垂直に通過したときの透過率を求めてみる。上述の透過率 $T$ に空気の屈折率 $n_1=1$ とガラスの屈折率 $n_2=1.5$ を代入すると、 $T=0.96$ が得られる。つまり、ガラス板の透過率は96%と計算される。しかし、実際に測ってみると透過率は約92%と少し小さい値になる。どこが間違っていただろうか？

ポイントは、フレネル係数が物質の境界だけでの反射と透過に注目しているところにある。光がガラス板を通過する過程には、空気からガラスへの透過と、ガラスから空気への透過の合計２回の透過が含まれる。言い換えると、光はガラス板の表面と裏面で2回反射するのである。したがって、透過率は $96\% \times 96\% = 92\%$ となる。ガラス１枚当たり92%減衰するということは、８枚透過すると光の強さは51%と半分程度になってしまうため、けっこう馬鹿にならない。